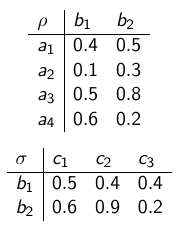
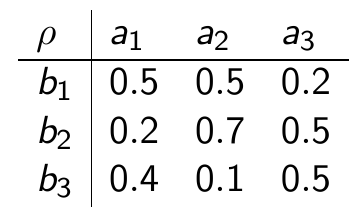
Пусть A = \{a_1,a_2,a_3\}, B = \{b_1,b_2,b_3\}, и отношение \rho задано матрицей
1.
Какой элемент A имеет наибольшее вхождение в \rho\left(\frac{0.6}{b_1}+\frac{0.4}{b_2}+\frac{0.7}{b_3}\right)?
В качестве нормы взять умножение, в качестве конормы - максимум.
1 балл
2. Какие из этих выражений имеют нечеткие логические значения?
1 балл
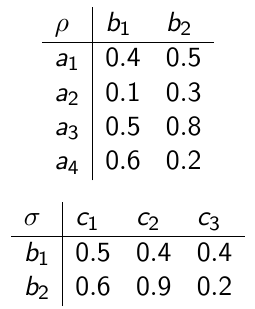
Пусть A=\{a_1,a_2, a_3, a_4\}, B=\{b_1,b_2\}, C=\{c_1,c_2,c_3\} \rho - нечеткое отношение на A\times B, \sigma - на B \times C, \tau=\rho\circ\sigma.
3.
Конорма - максимум, норма - произведение. Вычислите \tau(a_2,c_2).
1 балл
Пусть A = \{a_1,a_2\}, B = \{b_1,b_2,b_3\}.

4.
Вычислите меру вхождения a_1 и a_2 для \rho\left(\frac{0.6}{b1}+\frac{0.4}{b2}\right). Норма - умножение, а конорма - a+b-ab.
1 балл
5.
Нечёткие логические переменные удовлетворяют свойству:
1 балл
6.
Пусть M и N - нечёткие множества, m - нечеткая переменная, a - мера вхождения переменной m в M, b - мера вхождения переменной m в N.
Тогда может быть справедливо следующее:
1 балл
7.
Пусть A,B,C - четкие множества и \rho\subset A\times B, \sigma\subset B\times C - четкие отношения.
Тогда \rho\circ\sigma =...
1 балл
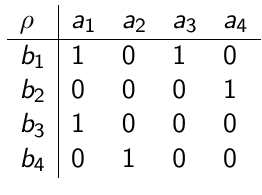
Пусть A={a_1,a_2,a_3,a_4}, B={b_1,b_2,b_3,b_4}, \rho\subset A\times B - четкое отношение.
8.
Выберите правильное описание для \rho и \rho^{-1}.
1 балл
9. В логике второго порядка становится возможным...
1 балл
Пусть A=\{a_1,a_2,a_3,a_4\}, B=\{b_1,b_2\}, C=\{c_1,c_2,c_3\}, \rho и \sigma — нечеткие отношения со следующими матрицами: